Draw Circle Using Sine and Cosine

To define our trigonometric functions, we begin past drawing a unit circumvolve, a circle centered at the origin with radius 1, equally shown in Effigy ii. The angle (in radians) that [latex]t[/latex] intercepts forms an arc of length [latex]s[/latex]. Using the formula [latex]s=rt[/latex], and knowing that [latex]r=ane[/latex], we run into that for a unit circumvolve, [latex]southward=t[/latex].

Think that the x- and y-axes divide the coordinate aeroplane into four quarters called quadrants. We label these quadrants to mimic the direction a positive bending would sweep. The four quadrants are labeled I, 2, Iii, and IV.

For any bending [latex]t[/latex], we can label the intersection of the final side and the unit circle equally past its coordinates, [latex]\left(x,y\right)[/latex]. The coordinates [latex]ten[/latex] and [latex]y[/latex] volition exist the outputs of the trigonometric functions [latex]f\left(t\right)=\cos t[/latex] and [latex]f\left(t\right)=\sin t[/latex], respectively. This means [latex]10=\cos t[/latex] and [latex]y=\sin t[/latex].

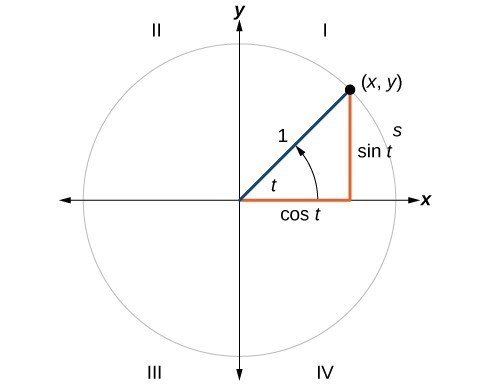
Figure 2. Unit circle where the central bending is [latex]t[/latex] radians

A General Note: Unit Circle

A unit circle has a center at [latex]\left(0,0\correct)[/latex] and radius [latex]1[/latex] . In a unit circumvolve, the length of the intercepted arc is equal to the radian measure of the central angle [latex]1[/latex].

Let [latex]\left(x,y\right)[/latex] be the endpoint on the unit circle of an arc of arc length [latex]s[/latex]. The [latex]\left(x,y\right)[/latex] coordinates of this point tin exist described as functions of the angle.

Defining Sine and Cosine Functions

Now that we have our unit circle labeled, we can learn how the [latex]\left(x,y\right)[/latex] coordinates chronicle to the arc length and angle. The sine office relates a real number [latex]t[/latex] to the y-coordinate of the indicate where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle [latex]t[/latex] equals the y-value of the endpoint on the unit circumvolve of an arc of length [latex]t[/latex]. In Effigy two, the sine is equal to [latex]y[/latex]. Like all functions, the sine office has an input and an output. Its input is the measure out of the bending; its output is the y-coordinate of the corresponding point on the unit circumvolve.

The cosine function of an angle [latex]t[/latex] equals the x-value of the endpoint on the unit circle of an arc of length [latex]t[/latex]. In Figure 3, the cosine is equal to [latex]x[/latex].

Figure 3

Considering it is understood that sine and cosine are functions, we do not always need to write them with parentheses: [latex]\sin t[/latex] is the same every bit [latex]\sin \left(t\right)[/latex] and [latex]\cos t[/latex] is the same as [latex]\cos \left(t\right)[/latex]. Likewise, [latex]{\cos }^{2}t[/latex] is a commonly used shorthand notation for [latex]{\left(\cos \left(t\right)\right)}^{2}[/latex]. Be enlightened that many calculators and computers do not recognize the autograph notation. When in doubt, use the extra parentheses when inbound calculations into a figurer or computer.

A Full general Note: Sine and Cosine Functions

If [latex]t[/latex] is a real number and a bespeak [latex]\left(10,y\right)[/latex] on the unit circumvolve corresponds to an angle of [latex]t[/latex], and so

[latex]\cos t=x[/latex]

[latex]\sin t=y[/latex]

How To: Given a point P [latex]\left(x,y\right)[/latex] on the unit circumvolve corresponding to an angle of [latex]t[/latex], discover the sine and cosine.

1. The sine of [latex]t[/latex] is equal to the y-coordinate of point [latex]P:\sin t=y[/latex].
2. The cosine of [latex]t[/latex] is equal to the 10-coordinate of point [latex]P: \text{cos}t=10[/latex].

Case one: Finding Role Values for Sine and Cosine

Betoken [latex]P[/latex] is a point on the unit circumvolve corresponding to an bending of [latex]t[/latex], as shown in Figure four. Detect [latex]\cos \left(t\right)\\[/latex] and [latex]\text{sin}\left(t\right)\\[/latex].

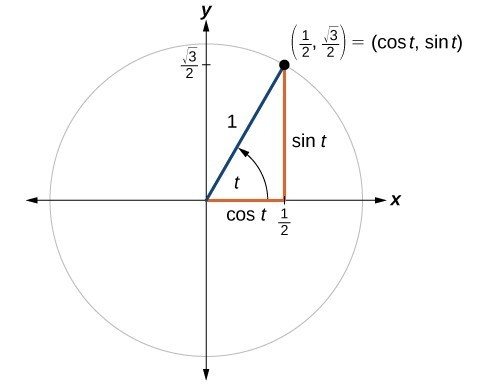
Effigy four

Solution

We know that [latex]\cos t[/latex] is the x-coordinate of the corresponding betoken on the unit circle and [latex]\sin t[/latex] is the y-coordinate of the corresponding point on the unit circle. And then:

[latex]\brainstorm{array}{l}\begin{array}{l}\\ ten=\cos t=\frac{1}{2}\end{array}\hfill \\ y=\sin t=\frac{\sqrt{3}}{two}\hfill \end{array}\\[/latex]

Endeavour Information technology 1

A certain angle [latex]t[/latex] corresponds to a bespeak on the unit circle at [latex]\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{ii}}{2}\right)\\[/latex] equally shown in Figure 5. Find [latex]\cos t[/latex] and [latex]\sin t[/latex].

Figure v

Solution

Finding Sines and Cosines of Angles on an Axis

For quadrantral angles, the respective betoken on the unit circumvolve falls on the x- or y-axis. In that case, we tin easily summate cosine and sine from the values of [latex]ten[/latex] and [latex]y[/latex].

Instance 2: Computing Sines and Cosines along an Axis

Detect [latex]\cos \left(90^\circ \right)\\[/latex] and [latex]\text{sin}\left(90^\circ \right)\\[/latex].

Solution

Moving [latex]xc^\circ [/latex] counterclockwise effectually the unit circle from the positive x-axis brings united states of america to the summit of the circle, where the [latex]\left(10,y\right)[/latex] coordinates are (0, one), every bit shown in Figure 6.

Figure half-dozen

Using our definitions of cosine and sine,

[latex]\begin{array}{l}x=\cos t=\cos \left(90^\circ \right)=0\\ y=\sin t=\sin \left(90^\circ \correct)=one\end{array}\\[/latex]

The cosine of 90° is 0; the sine of 90° is i.

Try It 2

Notice cosine and sine of the angle [latex]\pi [/latex].

Solution

The Pythagorean Identity

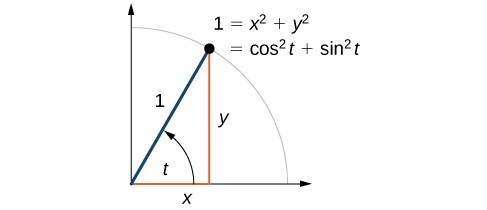
Figure 7

Now that we can define sine and cosine, we volition learn how they chronicle to each other and the unit of measurement circle. Recollect that the equation for the unit circumvolve is [latex]{x}^{2}+{y}^{2}=1[/latex]. Because [latex]ten=\cos t[/latex] and [latex]y=\sin t[/latex], nosotros tin can substitute for [latex]10[/latex] and [latex]y[/latex] to get [latex]{\cos }^{ii}t+{\sin }^{ii}t=1[/latex]. This equation, [latex]{\cos }^{2}t+{\sin }^{2}t=one[/latex], is known as the Pythagorean Identity.

We can use the Pythagorean Identity to notice the cosine of an bending if we know the sine, or vice versa. However, because the equation yields two solutions, we demand additional knowledge of the angle to cull the solution with the correct sign. If nosotros know the quadrant where the bending is, we can easily cull the correct solution.

A General Note: Pythagorean Identity

The Pythagorean Identity states that, for any real number [latex]t[/latex],

[latex]{\cos }^{two}t+{\sin }^{2}t=one[/latex]

How To: Given the sine of some angle [latex]t[/latex] and its quadrant location, find the cosine of [latex]t[/latex].

1. Substitute the known value of [latex]\sin \left(t\right)[/latex] into the Pythagorean Identity.
2. Solve for [latex]\cos \left(t\right)[/latex].
3. Cull the solution with the appropriate sign for the x-values in the quadrant where [latex]t[/latex] is located.

Example 3: Finding a Cosine from a Sine or a Sine from a Cosine

If [latex]\sin \left(t\right)=\frac{three}{vii}\\[/latex] and [latex]t[/latex] is in the 2d quadrant, find [latex]\cos \left(t\right)\\[/latex].

Solution

If nosotros drop a vertical line from the point on the unit circle respective to [latex]t[/latex], we create a right triangle, from which we can see that the Pythagorean Identity is just i instance of the Pythagorean Theorem.

Figure 8

Substituting the known value for sine into the Pythagorean Identity,

[latex]\brainstorm{assortment}{50}{\cos }^{2}\left(t\right)+{\sin }^{2}\left(t\right)=1\hfill \\ {\cos }^{2}\left(t\right)+\frac{9}{49}=1\hfill \\ {\cos }^{2}\left(t\correct)=\frac{40}{49}\hfill \\ \text{cos}\left(t\right)=\pm \sqrt{\frac{40}{49}}=\pm \frac{\sqrt{40}}{7}=\pm \frac{two\sqrt{x}}{7}\hfill \end{array}\\[/latex]

Because the angle is in the second quadrant, we know the x-value is a negative existent number, and so the cosine is also negative. Then
[latex]\text{cos}\left(t\right)=-\frac{2\sqrt{x}}{vii}\\[/latex]

Try Information technology 3

If [latex]\cos \left(t\right)=\frac{24}{25}\\[/latex] and [latex]t[/latex] is in the fourth quadrant, detect [latex]\text{sin}\left(t\correct)\\[/latex].

Solution

Finding Sines and Cosines of Special Angles

We accept already learned some properties of the special angles, such as the conversion from radians to degrees. We can also summate sines and cosines of the special angles using the Pythagorean Identity and our cognition of triangles.

Finding Sines and Cosines of 45° Angles

First, we will await at angles of [latex]45^\circ [/latex] or [latex]\frac{\pi }{4}[/latex], as shown in Effigy nine. A [latex]45^\circ -45^\circ -90^\circ [/latex] triangle is an isosceles triangle, so the x- and y-coordinates of the corresponding point on the circle are the same. Because the x- and y-values are the same, the sine and cosine values will also exist equal.

Figure nine

At [latex]t=\frac{\pi }{4}[/latex] , which is 45 degrees, the radius of the unit circumvolve bisects the first quadrantal bending. This means the radius lies forth the line [latex]y=x[/latex]. A unit of measurement circle has a radius equal to i. So, the right triangle formed below the line [latex]y=x[/latex] has sides [latex]x[/latex] and [latex]y\text{ }\left(y=x\right)[/latex], and a radius = 1.

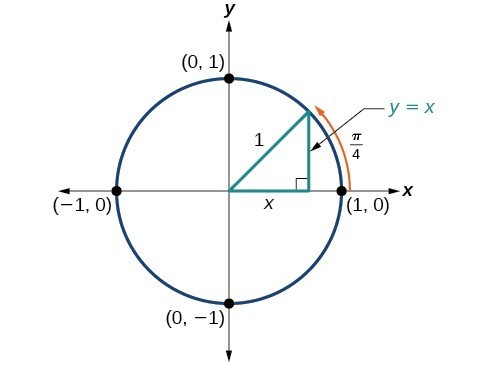
Figure 10

From the Pythagorean Theorem nosotros get

[latex]{x}^{2}+{y}^{two}=1[/latex]

Substituting [latex]y=x[/latex], nosotros become

[latex]{ten}^{2}+{x}^{2}=1[/latex]

Combining similar terms we get

[latex]2{x}^{2}=1[/latex]

And solving for [latex]ten[/latex], we become

[latex]\begin{assortment}{c}{x}^{2}=\frac{1}{2}\\ \text{ }x=\pm \frac{1}{\sqrt{two}}\end{assortment}\\[/latex]

In quadrant I, [latex]x=\frac{1}{\sqrt{2}}\\[/latex].

At [latex]t=\frac{\pi }{four}[/latex] or 45 degrees,

[latex]\begin{array}{50}\left(x,y\right)=\left(x,x\right)=\left(\frac{one}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\hfill \\ x=\frac{1}{\sqrt{2}},y=\frac{1}{\sqrt{two}}\hfill \\ \cos t=\frac{ane}{\sqrt{2}},\sin t=\frac{one}{\sqrt{two}}\hfill \end{assortment}\\[/latex]

If we then rationalize the denominators, we get

[latex]\brainstorm{array}{fifty}\cos t=\frac{1}{\sqrt{2}}\frac{\sqrt{2}}{\sqrt{ii}}\hfill \\ =\frac{\sqrt{ii}}{2}\hfill \\ \sin t=\frac{1}{\sqrt{2}}\frac{\sqrt{two}}{\sqrt{2}}\hfill \\ =\frac{\sqrt{two}}{2}\hfill \end{array}\\[/latex]

Therefore, the [latex]\left(10,y\right)\\[/latex] coordinates of a point on a circle of radius [latex]1[/latex] at an angle of [latex]45^\circ [/latex] are [latex]\left(\frac{\sqrt{two}}{two},\frac{\sqrt{2}}{2}\correct)\\[/latex].

Finding Sines and Cosines of 30° and lx° Angles

Next, nosotros will find the cosine and sine at an angle of [latex]xxx^\circ [/latex], or [latex]\frac{\pi }{6}\\[/latex] . First, we will draw a triangle inside a circumvolve with one side at an angle of [latex]30^\circ [/latex], and another at an angle of [latex]-thirty^\circ [/latex], as shown in Figure 11. If the resulting two correct triangles are combined into one large triangle, notice that all 3 angles of this larger triangle will be [latex]60^\circ [/latex], every bit shown in Figure 12.

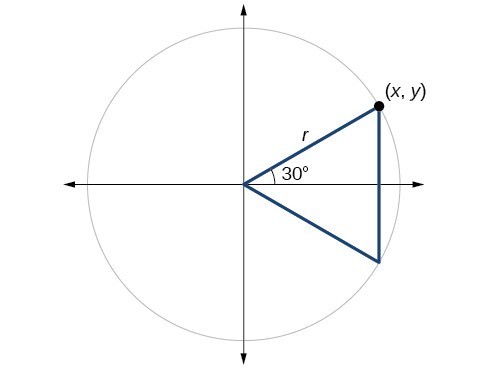
Figure 11

Figure 12

Because all the angles are equal, the sides are also equal. The vertical line has length [latex]2y[/latex], and since the sides are all equal, we can besides conclude that [latex]r=2y[/latex] or [latex]y=\frac{one}{2}r[/latex]. Since [latex]\sin t=y[/latex] ,

[latex]\sin \left(\frac{\pi }{6}\right)=\frac{ane}{ii}r\\[/latex]

And since [latex]r=ane[/latex] in our unit circle,

[latex]\begin{array}{l}\sin \left(\frac{\pi }{six}\right)=\frac{1}{ii}\left(ane\right)\hfill \\ \text{ }=\frac{1}{2}\hfill \end{array}\\[/latex]

Using the Pythagorean Identity, we can find the cosine value.

[latex]\begin{array}{ll}{\cos }^{2}\frac{\pi }{half-dozen}+{\sin }^{ii}\left(\frac{\pi }{6}\correct)=one\hfill & \hfill \\ \text{ }{\cos }^{2}\left(\frac{\pi }{6}\correct)+{\left(\frac{i}{2}\right)}^{2}=1\hfill & \hfill \\ \text{ }{\cos }^{2}\left(\frac{\pi }{half dozen}\right)=\frac{iii}{4}\hfill & \text{Use the square root property}.\hfill \\ \text{ }\cos \left(\frac{\pi }{6}\right)=\frac{\pm \sqrt{3}}{\pm \sqrt{iv}}=\frac{\sqrt{three}}{ii}\hfill & \text{Since }y\text{ is positive, choose the positive root}.\hfill \end{array}\\[/latex]

The [latex]\left(x,y\right)[/latex] coordinates for the point on a circle of radius [latex]1[/latex] at an angle of [latex]30^\circ [/latex] are [latex]\left(\frac{\sqrt{iii}}{2},\frac{1}{2}\correct)\\[/latex]. At [latex]t=\frac{\pi }{iii}[/latex] (60°), the radius of the unit circle, one, serves as the hypotenuse of a thirty-60-90 degree correct triangle, [latex]BAD[/latex], as shown in [link]. Bending [latex]A[/latex] has measure out [latex]60^\circ [/latex]. At betoken [latex]B[/latex], we describe an angle [latex]ABC[/latex] with mensurate of [latex]lx^\circ [/latex]. We know the angles in a triangle sum to [latex]180^\circ [/latex], so the measure out of angle [latex]C[/latex] is too [latex]60^\circ [/latex]. Now we take an equilateral triangle. Because each side of the equilateral triangle [latex]ABC[/latex] is the aforementioned length, and nosotros know one side is the radius of the unit circle, all sides must be of length 1.

Figure 13

The measure of bending [latex]ABD[/latex] is 30°. So, if double, angle [latex]ABC[/latex] is 60°. [latex]BD[/latex] is the perpendicular bisector of [latex]Ac[/latex], then information technology cuts [latex]AC[/latex] in half. This means that [latex]AD[/latex] is [latex]\frac{ane}{2}[/latex] the radius, or [latex]\frac{1}{ii}[/latex]. Notice that [latex]AD[/latex] is the 10-coordinate of point [latex]B[/latex], which is at the intersection of the 60° bending and the unit circumvolve. This gives us a triangle [latex]BAD[/latex] with hypotenuse of 1 and side [latex]10[/latex] of length [latex]\frac{1}{two}\\[/latex].

From the Pythagorean Theorem, we get

[latex]{x}^{two}+{y}^{two}=1[/latex]

Substituting [latex]x=\frac{1}{two}[/latex], nosotros become

[latex]{\left(\frac{1}{ii}\right)}^{2}+{y}^{2}=i[/latex]

Solving for [latex]y[/latex], nosotros go

[latex]\begin{assortment}{l}\frac{1}{4}+{y}^{two}=one\\ \text{ }{y}^{2}=i-\frac{1}{four}\\ \text{ }{y}^{2}=\frac{3}{4}\\ \text{ }y=\pm \frac{\sqrt{iii}}{2}\end{assortment}\\[/latex]

Since [latex]t=\frac{\pi }{3}[/latex] has the final side in quadrant I where the y-coordinate is positive, we choose [latex]y=\frac{\sqrt{3}}{2}\\[/latex], the positive value.

At [latex]t=\frac{\pi }{3}\\[/latex] (lx°), the [latex]\left(ten,y\right)[/latex] coordinates for the point on a circumvolve of radius [latex]1[/latex] at an angle of [latex]lx^\circ [/latex] are [latex]\left(\frac{ane}{two},\frac{\sqrt{three}}{two}\right)\\[/latex], then nosotros tin detect the sine and cosine.

[latex]\begin{array}{fifty}\left(x,y\right)=\left(\frac{one}{2},\frac{\sqrt{three}}{2}\right)\hfill \\ x=\frac{1}{ii},y=\frac{\sqrt{3}}{two}\hfill \\ \cos t=\frac{1}{2},\sin t=\frac{\sqrt{3}}{2}\hfill \finish{array}\\[/latex]

Nosotros accept now found the cosine and sine values for all of the well-nigh ordinarily encountered angles in the offset quadrant of the unit of measurement circle. The tabular array beneath summarizes these values.

Angle	0	[latex]\frac{\pi }{half dozen}\\[/latex], or 30	[latex]\frac{\pi }{four}\\[/latex], or 45°	[latex]\frac{\pi }{3}\\[/latex], or sixty°	[latex]\frac{\pi }{2}\\[/latex], or 90°
Cosine	1	[latex]\frac{\sqrt{iii}}{2}\\[/latex]	[latex]\frac{\sqrt{ii}}{two}\\[/latex]	[latex]\frac{one}{2}\\[/latex]	0
Sine	0	[latex]\frac{1}{2}\\[/latex]	[latex]\frac{\sqrt{2}}{2}\\[/latex]	[latex]\frac{\sqrt{iii}}{ii}\\[/latex]	1

Figure 14 shows the common angles in the first quadrant of the unit of measurement circumvolve.

Figure fourteen

Using a Calculator to Find Sine and Cosine

To notice the cosine and sine of angles other than the special angles, nosotros turn to a computer or calculator. Exist aware: Most calculators can be set into "degree" or "radian" mode, which tells the estimator the units for the input value. When we evaluate [latex]\cos \left(thirty\right)[/latex] on our computer, it will evaluate it every bit the cosine of thirty degrees if the figurer is in caste style, or the cosine of 30 radians if the computer is in radian mode.

How To: Given an angle in radians, use a graphing calculator to find the cosine.

1. If the computer has caste fashion and radian way, prepare it to radian mode.
2. Press the COS key.
3. Enter the radian value of the angle and press the close-parentheses key ")".
4. Press ENTER.

Example 4: Using a Graphing Computer to Discover Sine and Cosine

Evaluate [latex]\cos \left(\frac{5\pi }{3}\correct)\\[/latex] using a graphing figurer or estimator.

Solution

Enter the following keystrokes:

COS (5 × π ÷ 3 ) ENTER

[latex]\cos \left(\frac{5\pi }{iii}\correct)=0.5\\[/latex]

Analysis of the Solution

We can find the cosine or sine of an angle in degrees straight on a calculator with degree manner. For calculators or software that employ simply radian mode, we tin can find the sign of [latex]20^\circ [/latex], for example, by including the conversion factor to radians as office of the input:

SIN( xx × π ÷ 180 ) ENTER

Effort It 4

Evaluate [latex]\sin \left(\frac{\pi }{iii}\right)\\[/latex].

Solution

Identifying the Domain and Range of Sine and Cosine Functions

Now that we can detect the sine and cosine of an angle, we demand to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that tin be inputs of the functions? Because angles smaller than 0 and angles larger than [latex]2\pi [/latex] tin still be graphed on the unit circle and have real values of [latex]x,y[/latex], and [latex]r[/latex], in that location is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive 10-axis, and that may be whatsoever existent number.

What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We tin can encounter the answers by examining the unit circle, as shown in Figure fifteen. The bounds of the x-coordinate are [latex]\left[-1,1\correct][/latex]. The bounds of the y-coordinate are also [latex]\left[-one,1\right][/latex]. Therefore, the range of both the sine and cosine functions is [latex]\left[-1,1\correct][/latex].

Figure 15

Nosotros accept discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in some other quadrant? For any given angle in the first quadrant, there is an bending in the second quadrant with the same sine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but accept the reverse x-value. Therefore, its cosine value volition exist the opposite of the first angle's cosine value.

Besides, there volition be an angle in the fourth quadrant with the aforementioned cosine as the original bending. The bending with the same cosine will share the same x-value but volition accept the opposite y-value. Therefore, its sine value volition be the opposite of the original angle's sine value.

As shown in Figure 16, bending [latex]\alpha [/latex] has the same sine value every bit bending [latex]t[/latex]; the cosine values are opposites. Bending [latex]\beta [/latex] has the same cosine value as angle [latex]t[/latex]; the sine values are opposites.

[latex]\begin{array}{lll}\sin \left(t\correct)=\sin \left(\blastoff \right)\hfill & \text{and}\hfill & \cos \left(t\right)=-\cos \left(\blastoff \right)\hfill \\ \sin \left(t\right)=-\sin \left(\beta \right)\hfill & \text{and}\hfill & \cos \left(t\right)=\cos \left(\beta \correct)\hfill \cease{array}[/latex]

Figure sixteen

Think that an angle'due south reference angle is the astute angle, [latex]t[/latex], formed by the final side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is e'er an angle betwixt [latex]0[/latex] and [latex]90^\circ [/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can come across from Figure 17, for any angle in quadrants Two, Iii, or Iv, there is a reference bending in quadrant I.

Figure 17

How To: Given an angle between [latex]0[/latex] and [latex]2\pi [/latex], notice its reference angle.

1. An angle in the first quadrant is its own reference bending.
2. For an angle in the 2nd or tertiary quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
3. For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
4. If an bending is less than [latex]0[/latex] or greater than [latex]two\pi [/latex], add or subtract [latex]2\pi [/latex] every bit many times as needed to find an equivalent bending between [latex]0[/latex] and [latex]2\pi [/latex].

Case 5: Finding a Reference Angle

Discover the reference angle of [latex]225^\circ [/latex] as shown in Figure 18.

Figure 18

Solution

Because [latex]225^\circ [/latex] is in the tertiary quadrant, the reference angle is

[latex]|\left(180^\circ -225^\circ \correct)|=|-45^\circ |=45^\circ [/latex]

Try It 5

Find the reference angle of [latex]\frac{5\pi }{3}[/latex].

Solution

Using Reference Angles

Now allow's take a moment to reconsider the Ferris wheel introduced at the start of this section. Suppose a rider snaps a photograph while stopped twenty feet in a higher place ground level. The passenger then rotates 3-quarters of the way around the circle. What is the rider's new elevation? To reply questions such as this 1, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles exterior the first quadrant. They tin also exist used to discover [latex]\left(10,y\right)[/latex] coordinates for those angles. We volition use the reference angle of the angle of rotation combined with the quadrant in which the concluding side of the angle lies.

Using Reference Angles to Evaluate Trigonometric Functions

We tin can find the cosine and sine of whatever angle in whatever quadrant if we know the cosine or sine of its reference bending. The absolute values of the cosine and sine of an bending are the same every bit those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the x-values in that quadrant. The sine volition exist positive or negative depending on the sign of the y-values in that quadrant.

A Full general Note: Using Reference Angles to Observe Cosine and Sine

Angles accept cosines and sines with the same accented value as their reference angles. The sign (positive or negative) tin can exist determined from the quadrant of the angle.

How To: Given an angle in standard position, detect the reference bending, and the cosine and sine of the original bending.

1. Measure the angle between the terminal side of the given bending and the horizontal centrality. That is the reference angle.
2. Determine the values of the cosine and sine of the reference angle.
3. Give the cosine the same sign equally the x-values in the quadrant of the original bending.
4. Requite the sine the same sign as the y-values in the quadrant of the original angle.

Example 5: Using Reference Angles to Discover Sine and Cosine

1. Using a reference angle, notice the exact value of [latex]\cos \left(150^\circ \correct)[/latex] and [latex]\text{sin}\left(150^\circ \right)[/latex].
2. Using the reference angle, observe [latex]\cos \frac{5\pi }{4}[/latex] and [latex]\sin \frac{5\pi }{4}[/latex].

Solution

1. 150° is located in the 2nd quadrant. The angle it makes with the x-axis is 180° − 150° = xxx°, so the reference angle is 30°.This tells united states of america that 150° has the same sine and cosine values as 30°, except for the sign. Nosotros know that

   [latex]\cos \left(30^\circ \correct)=\frac{\sqrt{3}}{2}\text{and}\sin \left(30^\circ \right)=\frac{1}{2}[/latex].

   Since 150° is in the 2d quadrant, the x-coordinate of the point on the circumvolve is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.

   [latex]\cos \left(150^\circ \right)=-\frac{\sqrt{3}}{ii}\text{and}\sin \left(150^\circ \right)=\frac{1}{ii}[/latex]

2. [latex]\frac{v\pi }{four}[/latex] is in the 3rd quadrant. Its reference angle is [latex]\frac{5\pi }{4}-\pi =\frac{\pi }{4}[/latex]. The cosine and sine of [latex]\frac{\pi }{4}[/latex] are both [latex]\frac{\sqrt{ii}}{2}[/latex]. In the third quadrant, both [latex]10[/latex] and [latex]y[/latex] are negative, so:

   [latex]\cos \frac{5\pi }{four}=-\frac{\sqrt{two}}{two}\text{and}\sin \frac{v\pi }{4}=-\frac{\sqrt{2}}{2}[/latex]

Endeavor Information technology half dozen

a. Apply the reference angle of [latex]315^\circ [/latex] to detect [latex]\cos \left(315^\circ \right)[/latex] and [latex]\sin \left(315^\circ \right)[/latex].

b. Use the reference angle of [latex]-\frac{\pi }{6}[/latex] to find [latex]\cos \left(-\frac{\pi }{6}\right)[/latex] and [latex]\sin \left(-\frac{\pi }{half-dozen}\right)[/latex].

Using Reference Angles to Find Coordinates

Now that nosotros take learned how to discover the cosine and sine values for special angles in the first quadrant, we can apply symmetry and reference angles to fill in cosine and sine values for the remainder of the special angles on the unit circumvolve. They are shown in Effigy 19. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant.

In improver to learning the values for special angles, nosotros tin can use reference angles to find [latex]\left(ten,y\right)[/latex] coordinates of any signal on the unit of measurement circle, using what we know of reference angles along with the identities

[latex]\brainstorm{array}{fifty}10=\cos t\hfill \\ y=\sin t\hfill \end{array}[/latex]

First we find the reference bending corresponding to the given bending. So nosotros accept the sine and cosine values of the reference angle, and give them the signs corresponding to the y– and x-values of the quadrant.

How To: Given the angle of a point on a circle and the radius of the circumvolve, notice the [latex]\left(x,y\correct)[/latex] coordinates of the point.

1. Find the reference angle by measuring the smallest angle to the 10-centrality.
2. Discover the cosine and sine of the reference angle.
3. Determine the appropriate signs for [latex]x[/latex] and [latex]y[/latex]
   in the given quadrant.

Example vi: Using the Unit Circumvolve to Find Coordinates

Find the coordinates of the point on the unit circle at an angle of [latex]\frac{vii\pi }{half-dozen}[/latex].

Solution

Nosotros know that the angle [latex]\frac{7\pi }{6}[/latex] is in the third quadrant.

First, allow's find the reference angle by measuring the angle to the 10-axis. To find the reference angle of an bending whose last side is in quadrant Iii, nosotros find the divergence of the angle and [latex]\pi [/latex].

[latex]\frac{7\pi }{6}-\pi =\frac{\pi }{half dozen}[/latex]

Adjacent, nosotros volition find the cosine and sine of the reference angle:

[latex]\cos \left(\frac{\pi }{6}\right)=\frac{\sqrt{iii}}{2}\sin \left(\frac{\pi }{half dozen}\right)=\frac{i}{2}[/latex]

We must determine the appropriate signs for x and y in the given quadrant. Because our original bending is in the third quadrant, where both [latex]x[/latex] and [latex]y[/latex] are negative, both cosine and sine are negative.

[latex]\begin{assortment}{l}\cos \left(\frac{7\pi }{6}\right)=-\frac{\sqrt{3}}{2}\hfill \\ \sin \left(\frac{7\pi }{vi}\right)=-\frac{1}{2}\hfill \end{array}[/latex]

Now we tin can calculate the [latex]\left(ten,y\correct)[/latex] coordinates using the identities [latex]ten=\cos \theta [/latex] and [latex]y=\sin \theta [/latex].

The coordinates of the signal are [latex]\left(-\frac{\sqrt{3}}{2},-\frac{ane}{two}\correct)[/latex] on the unit circumvolve.

Try It 7

Find the coordinates of the indicate on the unit circumvolve at an bending of [latex]\frac{5\pi }{iii}[/latex].

Solution

Key Equations

Cosine	[latex]\cos t=x[/latex]
Sine	[latex]\sin t=y[/latex]
Pythagorean Identity	[latex]{\cos }^{ii}t+{\sin }^{2}t=1[/latex]

Central Concepts

• Finding the function values for the sine and cosine begins with drawing a unit circumvolve, which is centered at the origin and has a radius of 1 unit.
• Using the unit circle, the sine of an angle [latex]t[/latex] equals the y-value of the endpoint on the unit circle of an arc of length [latex]t[/latex] whereas the cosine of an bending [latex]t[/latex] equals the ten-value of the endpoint.
• The sine and cosine values are nigh direct determined when the respective point on the unit circle falls on an axis.
• When the sine or cosine is known, we tin use the Pythagorean Identity to find the other. The Pythagorean Identity is also useful for determining the sines and cosines of special angles.
• Calculators and graphing software are helpful for finding sines and cosines if the proper procedure for entering information is known.
• The domain of the sine and cosine functions is all real numbers.
• The range of both the sine and cosine functions is [latex]\left[-1,ane\right][/latex].
• The sine and cosine of an bending take the aforementioned absolute value every bit the sine and cosine of its reference bending.
• The signs of the sine and cosine are determined from the x– and y-values in the quadrant of the original angle.
• An angle's reference angle is the size angle, [latex]t[/latex],
  formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis.
• Reference angles tin can exist used to observe the sine and cosine of the original bending.
• Reference angles can also exist used to find the coordinates of a point on a circumvolve.

Glossary

cosine function

the ten-value of the signal on a unit circle respective to a given bending

Pythagorean Identity

a corollary of the Pythagorean Theorem stating that the square of the cosine of a given angle plus the square of the sine of that bending equals 1

sine function

the y-value of the point on a unit circle corresponding to a given angle

unit circumvolve

a circle with a heart at [latex]\left(0,0\right)[/latex]
and radius

Department Exercises

one. Describe the unit of measurement circle.

ii. What do the x- and y-coordinates of the points on the unit circle represent?

three. Discuss the difference between a coterminal angle and a reference angle.

4. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit of measurement circumvolve.

5. Explain how the sine of an angle in the second quadrant differs from the sine of its reference bending in the unit circumvolve.

For the following exercises, use the given sign of the sine and cosine functions to discover the quadrant in which the concluding point determined by [latex]t[/latex] lies.

6. [latex]\text{sin}\left(t\right)<0[/latex] and [latex]\text{cos}\left(t\right)<0[/latex]

7. [latex]\text{sin}\left(t\right)>0[/latex] and [latex]\cos \left(t\correct)>0[/latex]

8. [latex]\sin \left(t\correct)>0[/latex] and [latex]\cos \left(t\correct)<0[/latex]

9. [latex]\sin \left(t\right)<0[/latex] and [latex]\cos \left(t\correct)>0[/latex]

For the post-obit exercises, notice the verbal value of each trigonometric office.

10. [latex]\sin \frac{\pi }{2}[/latex]

11. [latex]\sin \frac{\pi }{3}[/latex]

12. [latex]\cos \frac{\pi }{two}[/latex]

13. [latex]\cos \frac{\pi }{3}[/latex]

xiv. [latex]\sin \frac{\pi }{4}[/latex]

15. [latex]\cos \frac{\pi }{4}[/latex]

xvi. [latex]\sin \frac{\pi }{6}[/latex]

17. [latex]\sin \pi [/latex]

18. [latex]\sin \frac{3\pi }{2}[/latex]

19. [latex]\cos \pi [/latex]

20. [latex]\cos 0[/latex]

21. [latex]\cos \frac{\pi }{6}[/latex]

22. [latex]\sin 0[/latex]

For the following exercises, state the reference angle for the given angle.

23. [latex]240^\circ [/latex]

24. [latex]-170^\circ [/latex]

25. [latex]100^\circ [/latex]

26. [latex]-315^\circ [/latex]

27. [latex]135^\circ [/latex]

28. [latex]\frac{5\pi }{4}[/latex]

29. [latex]\frac{2\pi }{3}[/latex]

30. [latex]\frac{5\pi }{6}[/latex]

31. [latex]\frac{-11\pi }{3}[/latex]

32. [latex]\frac{-7\pi }{iv}[/latex]

33. [latex]\frac{-\pi }{viii}[/latex]

For the following exercises, detect the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not 1 of the angles on the unit circle, employ a calculator and round to three decimal places.

34. [latex]225^\circ [/latex]

35. [latex]300^\circ [/latex]

36. [latex]320^\circ [/latex]

37. [latex]135^\circ [/latex]

38. [latex]210^\circ [/latex]

39. [latex]120^\circ [/latex]

40. [latex]250^\circ [/latex]

41. [latex]150^\circ [/latex]

42. [latex]\frac{v\pi }{four}[/latex]

43. [latex]\frac{7\pi }{half dozen}[/latex]

44. [latex]\frac{5\pi }{three}[/latex]

45. [latex]\frac{3\pi }{four}[/latex]

46. [latex]\frac{4\pi }{three}[/latex]

47. [latex]\frac{ii\pi }{3}[/latex]

48. [latex]\frac{5\pi }{half-dozen}[/latex]

49. [latex]\frac{7\pi }{4}[/latex]

For the post-obit exercises, find the requested value.

50. If [latex]\text{cos}\left(t\right)=\frac{one}{vii}[/latex] and [latex]t[/latex] is in the 4^thursday quadrant, find [latex]\text{sin}\left(t\correct)[/latex].

51. If [latex]\text{cos}\left(t\correct)=\frac{ii}{9}[/latex] and [latex]t[/latex] is in the 1^st quadrant, observe [latex]\text{sin}\left(t\right)[/latex].

52. If [latex]\text{sin}\left(t\right)=\frac{3}{eight}[/latex] and [latex]t[/latex] is in the ii^nd quadrant, find [latex]\text{cos}\left(t\right)[/latex].

53. If [latex]\text{sin}\left(t\correct)=-\frac{1}{4}[/latex] and [latex]t[/latex] is in the 3^rd quadrant, find [latex]\text{cos}\left(t\right)[/latex].

54. Observe the coordinates of the point on a circle with radius 15 corresponding to an angle of [latex]220^\circ [/latex].

55. Find the coordinates of the bespeak on a circle with radius twenty respective to an angle of [latex]120^\circ [/latex].

56. Find the coordinates of the point on a circumvolve with radius 8 respective to an angle of [latex]\frac{7\pi }{iv}[/latex].

57. Find the coordinates of the point on a circumvolve with radius 16 respective to an angle of [latex]\frac{5\pi }{9}[/latex].

58. Country the domain of the sine and cosine functions.

59. State the range of the sine and cosine functions.

For the following exercises, use the given point on the unit circumvolve to observe the value of the sine and cosine of [latex]t[/latex].

60.

61.

62.

63.

64.

65.

66.

67.

68.

69.

70.

71.

72.

73.

74.

75.

76.

77.

78.

79.

For the following exercises, employ a graphing calculator to evaluate.

80. [latex]\sin \frac{five\pi }{9}[/latex]

81. [latex]\cos \frac{5\pi }{ix}[/latex]

82. [latex]\sin \frac{\pi }{x}[/latex]

83. [latex]\cos \frac{\pi }{10}[/latex]

84. [latex]\sin \frac{iii\pi }{four}[/latex]

85. [latex]\cos \frac{iii\pi }{4}[/latex]

86. [latex]\sin 98^\circ [/latex]

87. [latex]\cos 98^\circ [/latex]

88. [latex]\cos 310^\circ [/latex]

89. [latex]\sin 310^\circ [/latex]

xc. [latex]\sin \left(\frac{eleven\pi }{3}\correct)\cos \left(\frac{-5\pi }{six}\correct)[/latex]

91. [latex]\sin \left(\frac{3\pi }{4}\right)\cos \left(\frac{five\pi }{three}\right)[/latex]

92. [latex]\sin \left(-\frac{4\pi }{3}\right)\cos \left(\frac{\pi }{ii}\right)[/latex]

93. [latex]\sin \left(\frac{-9\pi }{4}\right)\cos \left(\frac{-\pi }{vi}\right)[/latex]

94. [latex]\sin \left(\frac{\pi }{6}\right)\cos \left(\frac{-\pi }{3}\right)[/latex]

95. [latex]\sin \left(\frac{7\pi }{4}\right)\cos \left(\frac{-2\pi }{3}\right)[/latex]

96. [latex]\cos \left(\frac{5\pi }{half dozen}\right)\cos \left(\frac{2\pi }{3}\correct)[/latex]

97. [latex]\cos \left(\frac{-\pi }{3}\correct)\cos \left(\frac{\pi }{4}\correct)[/latex]

98. [latex]\sin \left(\frac{-5\pi }{4}\correct)\sin \left(\frac{11\pi }{six}\correct)[/latex]

99. [latex]\sin \left(\pi \right)\sin \left(\frac{\pi }{half dozen}\right)[/latex]

For the following exercises, use this scenario: A child enters a carousel that takes one infinitesimal to circumduct once effectually. The child enters at the point [latex]\left(0,1\right)[/latex], that is, on the due northward position. Assume the carousel revolves counter clockwise.

100. What are the coordinates of the child later 45 seconds?

101. What are the coordinates of the kid after ninety seconds?

102. What is the coordinates of the child after 125 seconds?

103. When volition the child take coordinates [latex]\left(0.707,-0.707\right)[/latex] if the ride lasts 6 minutes? (There are multiple answers.)

104. When will the child have coordinates [latex]\left(-0.866,-0.five\right)[/latex] if the ride terminal 6 minutes?

friersonpicketwor.blogspot.com

Source: https://courses.lumenlearning.com/precalctwo/chapter/unit-circle-sine-and-cosine-functions/

Share this post